Harmonic Analysis: Peter-Weyl Theorem and Machine Learning

The Peter-Weyl theorem is one of the most beautiful results in Harmonic Analysis, and it has found surprisingly wide applications in machine learning (drug discovery, molecular dynamics, robotics, particle physics, graphs, etc).

In many real-world problems, data is scarce, complexity is high, or we simply want our models to generalize better and produce more robust solutions. In these cases, it makes sense to leverage any prior knowledge we have about the problem structure. For example, in meteorology the data lives on a sphere (the Earth), or we might know that the underlying dynamics roughly satisfy the Navier-Stokes equations. The desire to incorporate this kind of domain-specific knowledge into machine learning models gave rise to what we now call Physics-Informed ML and Geometry-Informed ML. The former led to Neural ODEs and Physics-Informed Neural Networks (PINNs), but in this post we focus on the latter.

One of the reasons Convolutional Neural Networks work so well is a mathematical property that allows the model to recognize patterns even when they are shifted along the x- or y-axis. This is known as translation invariance (or equivariance), and we owe it to the convolution operation.

What’s interesting is that this same idea generalizes far beyond translation. It extends to arbitrary symmetries (rotations, reflections, permutations, etc) and to spaces beyond Euclidean geometry, such as graphs (giving us Graph Convolutional Networks). In full generality, it applies to locally compact groups.

In this post, we explore the theorem that makes all of this possible, and walk through how to compute the convolution on two concrete examples: SO(2) and SO(3).

1. Preliminaries

We start by introducing some basic notions from representation theory and harmonic analysis on compact groups.

Let $G$ be a locally compact group with a fixed (left) Haar measure $\mu$.

Definition (Unitary representation). A (unitary) representation of $G$ is a continuous homomorphism $\pi:G\to \mathfrak{U}(\mathcal{H}_\pi)$, where $\mathfrak{U}(\mathcal{H}_\pi)$ is the unitary group of a complex Hilbert space $\mathcal{H}_\pi$.

Equivalently, $\pi(gh)=\pi(g)\pi(h)$ for all $g,h\in G$ and $g\mapsto \pi(g)\xi$ is continuous for every $\xi\in \mathcal{H}_\pi$.

We denote $d_\pi:=\dim(\mathcal{H}_\pi)\in \mathbb{Z}_{\ge 0}\cup\{\infty\}$.

For compact $G$, one often starts with (not necessarily unitary) finite-dimensional representations $\pi:G\to \mathrm{GL}(V)$. In that case, averaging an inner product over Haar measure produces a $G$-invariant inner product, so every continuous finite-dimensional representation is equivalent to a unitary one.

Example (Left regular representation). On $\mathcal{H}:=L^2(G)$, the left regular representation $\lambda:G\to \mathfrak{U}(\mathcal{H})$ is defined by

$$ (\lambda(g)f)(x):=f(g^{-1}x),\qquad f\in L^2(G). $$

Definition (Equivalence). Two unitary representations $\pi_1:G\to\mathfrak{U}(\mathcal{H}_1)$ and $\pi_2:G\to\mathfrak{U}(\mathcal{H}_2)$ are equivalent if there exists a unitary $U:\mathcal{H}_1\to\mathcal{H}_2$ such that

$$ U\pi_1(g)=\pi_2(g)U,\qquad \forall g\in G. $$

We write $\pi_1\cong \pi_2$ and denote by $[\pi]$ the equivalence class of $\pi$.

Definition (Irreducible). A unitary representation $\pi:G\to\mathfrak{U}(\mathcal{H}_\pi)$ is irreducible if the only closed subspaces of $\mathcal{H}_\pi$ invariant under every $\pi(g)$ are $\{0\}$ and $\mathcal{H}_\pi$.

We denote by $\widehat{G}$ the set of equivalence classes of irreducible unitary representations of $G$.

If $G$ is abelian, then every irreducible unitary representation is one-dimensional; in particular, $\widehat{G}$ coincides with the character group (Pontryagin dual) of $G$.

Given representations $\pi$ and $\eta$, the tensor product representation $\pi\otimes \eta$ acts on $\mathcal{H}_\pi\otimes \mathcal{H}_\eta$ via

If $n\in \mathbb{Z}^+\cup\{\infty\}$, then $n\cdot \pi:=\bigoplus_{i=1}^n \pi$ denotes the direct sum of $n$ copies of $\pi$.

Definition (Commutant). If $\pi$ is a unitary representation of $G$, then

$$ \pi(G)' := \{A\in \mathcal{B}(\mathcal{H}_\pi) : A\pi(g)=\pi(g)A,\ \forall g\in G\} $$

is a *-subalgebra of $\mathcal{B}(\mathcal{H}_\pi)$ called the commutant of $\pi(G)$.

Theorem (Schur’s lemma / commutant characterization). For a unitary representation $\pi$, the following are equivalent:

1. $\pi$ is irreducible.
2. $\pi(G)'=\mathbb{C}I$.
3. Every nonzero $\xi\in \mathcal{H}_\pi$ is cyclic, i.e. $$ \overline{\mathrm{span}}\{\pi(g)\xi:g\in G\}=\mathcal{H}_\pi. $$

Proof. (1)$\Rightarrow$(2): Let $A\in \pi(G)'$. The real and imaginary parts of $A$ are self-adjoint and still commute with $\pi(G)$, so it suffices to consider self-adjoint $A$. If $A$ is not a scalar multiple of the identity, the spectral theorem produces a nontrivial spectral projection $P$ of $A$ (e.g. $P=\mathbf{1}_{(-\infty,t]}(A)$ for a suitable $t$). Since $P$ is a Borel functional calculus of $A$, it also commutes with $\pi(G)$; hence $\mathrm{ran}(P)$ is a nontrivial closed $\pi$-invariant subspace, contradicting irreducibility.

(2)$\Rightarrow$(1): If $W\subseteq \mathcal{H}_\pi$ is a nontrivial closed $\pi$-invariant subspace, the orthogonal projection $P_W$ belongs to $\pi(G)'$. By (2), $P_W$ must be $0$ or $I$, contradiction.

(1)$\Leftrightarrow$(3): For $\xi\neq 0$, the cyclic subspace $\overline{\mathrm{span}}\{\pi(g)\xi:g\in G\}$ is a nonzero closed invariant subspace, so it equals $\mathcal{H}_\pi$ iff $\pi$ is irreducible. $\square$

2. Peter-Weyl Theorem

In this section we specialize to compact groups. A locally compact group $G$ is compact iff $\mu(G)<\infty$; in that case Haar measure can be normalized uniquely by requiring $\mu(G)=1$. With this normalization we write

for integration against Haar measure.

2.1. Matrix coefficients and the coefficient space

Let $\pi$ be a finite-dimensional unitary representation of $G$ on $\mathcal{H}_\pi$ and let $\{e_1,\dots,e_{d_\pi}\}$ be an orthonormal basis. The functions

are called the matrix coefficients (or coordinate functions) of $\pi$.

More generally, for any $\xi,\eta\in \mathcal{H}_\pi$ the function $g\mapsto \langle \xi,\pi(g)\eta\rangle$ is continuous.

Definition (Coefficient space). Let $E_G$ be the linear span of all functions of the form

$$ g\mapsto \langle \xi,\pi(g)\eta\rangle, $$

where $\pi$ ranges over all irreducible unitary representations of $G$ and $\xi,\eta\in\mathcal{H}_\pi$.

We will write $E:=E_G$ when $G$ is clear.

Since every finite-dimensional unitary representation of a compact group decomposes as a direct sum of irreducibles, every matrix coefficient coming from an arbitrary finite-dimensional representation belongs to $E$.

Remark (Abelian case and trigonometric polynomials).
When $G$ is abelian, the functions in $E$ are often called trigonometric polynomials. For example, if

$$ G=\mathbb{T}=\mathbb{R}/2\pi\mathbb{Z}, $$

then every $f\in E$ has the form

$$ f(\theta)=\sum_{n=-N}^N c_n e^{in\theta} = \sum_{n=0}^N \bigl(a_n\cos(n\theta)+b_n\sin(n\theta)\bigr). $$

Remark (Conjugation and inversion).
If $f\in E$, then $\overline{f}\in E$. In terms of coordinate functions,

$$ \overline{\varphi_{ij}^{\pi}(g)} =\overline{\langle e_i,\pi(g)e_j\rangle} =\langle \pi(g)e_j,e_i\rangle =\langle e_j,\pi(g^{-1})e_i\rangle =\varphi_{ji}^\pi(g^{-1}). $$

In particular, if $f\in E$, then $\widetilde f(g):=f(g^{-1})$ also lies in $E$ (e.g. by passing to the contragredient representation). The same argument works inside $E_{\mathrm{fin}}$, since the contragredient of a finite-dimensional representation is again finite-dimensional.

2.2. Hilbert-Schmidt norms

Definition (Hilbert-Schmidt norm). Let $M_n$ be the complex $n\times n$ matrices. If $A=(a_{ij})\in M_n$, define the Hilbert-Schmidt norm by

$$ \|A\|_{\mathrm{HS}}^2=\sum_{i,j}|a_{ij}|^2. $$

Remark. If $A\in M_n$, then

$$ \|A\|_{\mathrm{HS}}^2=\mathrm{tr}(AA^*). $$

In particular, if $B=UAU^*$ for a unitary matrix $U$, then $\|A\|_{\mathrm{HS}}=\|B\|_{\mathrm{HS}}$. Hence, if $\pi$ is finite-dimensional, the value $\|\pi(g)\|_{\mathrm{HS}}$ depends only on the equivalence class $[\pi]$.

2.3. Statement of the Peter-Weyl theorem

Our goal is to prove the following result.

Theorem (Peter-Weyl). Let $G$ be a compact group.

1. Every irreducible unitary representation of $G$ is finite-dimensional.
2. If $\lambda$ is the left regular representation of $G$ on $L^2(G)$, then $$ \lambda \;\cong\; \bigoplus_{[\pi]\in \widehat{G}} d_\pi\cdot \pi. $$
3. (Separation of points) Given $g\in G$ with $g\ne e$, there exists $[\pi]\in\widehat G$ such that $\pi(g)\ne I$.
4. The space $E$ is dense in $C(G)$ (hence also dense in $L^p(G)$ for all $1\le p<\infty$).
5. (Plancherel / Parseval identity) If $f\in L^2(G)$, then $$ \|f\|_2^2 = \sum_{[\pi]\in\widehat G} d_\pi\,\mathrm{tr}\bigl(\widehat f(\pi)\,\widehat f(\pi)^*\bigr) = \sum_{[\pi]\in\widehat G} d_\pi \|\widehat f(\pi)\|_{\mathrm{HS}}^2, $$ where the operator-valued Fourier transform $\widehat f(\pi)$ is defined by $$ \widehat f(\pi)\;:=\;\int_G f(g)\,\pi(g^{-1})\,dg \quad\in\mathcal{B}(\mathcal{H}_\pi). $$

We will prove this theorem using a sequence of preliminary results.

2.4. Intertwiners and invariant subspaces

Lemma 1 (Adjoints of intertwiners). Let $\pi$ and $\eta$ be unitary representations of a locally compact group $G$. If $A:\mathcal{H}_\pi\to\mathcal{H}_\eta$ is bounded and satisfies

$$ A\pi(g)=\eta(g)A,\qquad \forall g\in G, $$

then $A^*$ also intertwines:

$$ A^*\eta(g)=\pi(g)A^*,\qquad \forall g\in G. $$

In particular, $A^*A\in \pi(G)'$ and $AA^*\in \eta(G)'$.

Proof. Taking adjoints in $A\pi(g)=\eta(g)A$ gives $\pi(g^{-1})A^*=A^*\eta(g^{-1})$, and since $\pi$ and $\eta$ are unitary this is equivalent to $A^*\eta(g)=\pi(g)A^*$. The commutant statements follow by multiplying by $A$ and $A^*$. $\square$

Lemma 2 (Nonzero intertwiners from irreducibles). Suppose $\pi$ and $\eta$ are unitary representations of a locally compact group $G$, with $\pi$ irreducible. If $A:\mathcal{H}_\pi\to\mathcal{H}_\eta$ is a nonzero bounded operator satisfying

$$ A\pi(g)=\eta(g)A,\qquad \forall g\in G, $$

then:

1. $A\mathcal{H}_\pi$ is a closed $\eta$-invariant subspace of $\mathcal{H}_\eta$;
2. $\pi\cong \eta|_{A\mathcal{H}_\pi}$.

Proof. By Lemma 1, $A^*A\in \pi(G)'$, so Schur’s lemma gives $A^*A=\lambda I$ for some $\lambda\ge 0$. Since $A\neq 0$, we have $\lambda>0$. Then $B:=\lambda^{-1/2}A$ satisfies $B^*B=I$, so $B$ is an isometry and $A\mathcal{H}_\pi=B\mathcal{H}_\pi$ is closed.

The intertwining identity implies $B\pi(g)=\eta(g)B$, so $B\mathcal{H}_\pi$ is $\eta$-invariant. Finally, $B$ is a unitary equivalence between $\pi$ and $\eta$ restricted to $B\mathcal{H}_\pi$. $\square$

2.5. Orthogonality relations

The next proposition is the key orthogonality statement for matrix coefficients, and it depends crucially on compactness of $G$.

Proposition (Schur orthogonality). Let $\pi$ and $\eta$ be irreducible finite-dimensional unitary representations of a compact group $G$. Fix orthonormal bases $\{e_i^\pi\}_{i=1}^{d_\pi}$ of $\mathcal{H}_\pi$ and $\{e_k^\eta\}_{k=1}^{d_\eta}$ of $\mathcal{H}_\eta$, and define

$$ \varphi_{ij}^\pi(g)=\langle e_i^\pi,\pi(g)e_j^\pi\rangle, \qquad \varphi_{kl}^\eta(g)=\langle e_k^\eta,\eta(g)e_l^\eta\rangle. $$

1. If $\pi\not\cong \eta$, then $$ \int_G \varphi_{ij}^\pi(g)\,\overline{\varphi_{kl}^\eta(g)}\,dg=0 \qquad\text{for all }i,j,k,l. $$
2. If $\pi\cong \eta$, then $$ \int_G \varphi_{ij}^\pi(g)\,\overline{\varphi_{kl}^\pi(g)}\,dg = \frac{\delta_{ik}\delta_{jl}}{d_\pi}, \qquad\text{for all }i,j,k,l. $$

Proof. Fix a bounded operator $B:\mathcal{H}_\pi\to\mathcal{H}_\eta$ and define

Since $\pi$ and $\eta$ are finite-dimensional, $g\mapsto \eta(g)B\pi(g^{-1})$ is continuous in operator norm, so the integral is well-defined (as a Bochner integral).

For $r\in G$, left invariance of Haar measure implies

so $A$ intertwines $\pi$ and $\eta$.

(1) If $\pi\not\cong\eta$, then Lemma 2 forces $A=0$. Fix indices $j,k$ and take the rank-one operator $B_{kj}(\xi)=\langle \xi,e_j^\pi\rangle e_k^\eta$. Then for any $i,l$,

using unitarity in the last step. Relabeling indices yields the desired orthogonality.

(2) Now assume $\pi=\eta$. Then $A\in \pi(G)'$, so by Schur’s lemma $A=\lambda I$ for some $\lambda\in \mathbb{C}$. Taking traces gives

so $\lambda=\mathrm{tr}(B)/d_\pi$. Taking $B=B_{jl}$ on $\mathcal{H}_\pi$ (i.e. $B_{jl}(\xi)=\langle \xi,e_l^\pi\rangle e_j^\pi$) gives $\lambda=\delta_{jl}/d_\pi$, and

$\square$

2.6. Proof of the Peter–Weyl theorem

Let $E_{\mathrm{fin}}\subseteq E$ denote the subspace spanned by matrix coefficients coming from finite-dimensional irreducible representations of $G$.

We first show that it suffices to prove that $E_{\mathrm{fin}}$ is dense in $C(G)$.

Assume $E_{\mathrm{fin}}$ is dense in $C(G)$. Since $C(G)$ is dense in $L^2(G)$, it follows that $E_{\mathrm{fin}}$ is also dense in $L^2(G)$.

For each irreducible $\pi$, Proposition (Schur orthogonality) shows that the $d_\pi^2$ functions $\{\sqrt{d_\pi}\,\varphi_{ij}^\pi\}_{i,j}$ form an orthonormal set in $L^2(G)$, and their linear span contains all matrix coefficients of $\pi$. Hence the closed span of all such normalized coefficients contains $E_{\mathrm{fin}}$, and therefore equals $L^2(G)$. In other words, these normalized matrix coefficients form an orthonormal basis of $L^2(G)$.

This already implies item (1): if there were an irreducible unitary representation $\sigma$ with $\dim(\mathcal{H}_\sigma)=\infty$, then the same averaging operator as in the proof of Schur orthogonality would produce an intertwiner $A:\mathcal{H}_\sigma\to \mathcal{H}_\pi$ for each finite-dimensional irreducible $\pi$. Any such nonzero $A$ would be injective (its kernel is a closed $\sigma$-invariant subspace), which is impossible into a finite-dimensional space. Hence $A=0$, so every matrix coefficient of $\sigma$ is orthogonal to every element of $E_{\mathrm{fin}}$. By density, all coefficients of $\sigma$ would have to be $0$, contradiction.

Now fix a finite-dimensional irreducible $\pi$ and let $H_\pi\subseteq L^2(G)$ be the closed span of its matrix coefficients (equivalently, the span of $\{\varphi_{ij}^\pi\}_{i,j}$).

Observe the standard coefficient identity: for $g,t\in G$,

For each fixed $j$, define a linear map $A_j:\mathcal{H}_\pi\to H_\pi$ by

Using the identity above, one checks that $A_j$ intertwines $\pi$ with the left regular representation $\lambda$ restricted to $H_\pi$:

By Schur orthogonality we have, for fixed $j$,

so $\widetilde A_j:=\sqrt{d_\pi}\,A_j$ is an isometry $\mathcal{H}_\pi\to L^2(G)$ and its range

is closed. Moreover, for $j\neq l$ the subspaces $H_{\pi,j}$ and $H_{\pi,l}$ are orthogonal. Hence

as an orthogonal direct sum of $\lambda$-invariant subspaces.

Since each $\widetilde A_j$ is a nonzero intertwiner from the irreducible representation $\pi$ into $\lambda|_{H_{\pi,j}}$, Lemma 2 yields $\lambda|_{H_{\pi,j}}\cong \pi$. Therefore

Summing over $[\pi]\in\widehat G$ yields item (2):

At this point we know $\{\sqrt{d_\pi}\,\varphi_{ij}^\pi\}$ is an orthonormal basis of $L^2(G)$, so every $f\in L^2(G)$ has an expansion

with

Moreover, by definition of Fourier coefficients in an orthonormal basis,

Therefore

which is item (5).

Item (3) follows from item (4): if $g\neq e$ and $\pi(g)=I$ for every irreducible $\pi$, then every matrix coefficient (hence every $f\in E$) would satisfy $f(g)=f(e)$, so $E$ could not be dense in $C(G)$.

Thus it only remains to prove:

Claim. $E_{\mathrm{fin}}$ is dense in $C(G)$.

We prove this using Hilbert–Schmidt operators and an approximate identity.

2.7. Hilbert–Schmidt operators and convolution

Let $(X,\nu)$ be a measure space and let $K\in L^2(X\times X,\nu\otimes\nu)$. Define an operator $T:L^2(X)\to L^2(X)$ by

Such operators are called Hilbert–Schmidt operators; they are compact, and if $K(x,y)=\overline{K(y,x)}$, then $T$ is self-adjoint. In particular, each eigenspace

is finite-dimensional.

In our case we take $X=G$ with normalized Haar measure and $K$ continuous. Then $x\mapsto K(x,\cdot)$ is continuous as a map into $L^2(G)$, and therefore $Tf(x)=\langle f, K(x,\cdot)\rangle_{L^2}$ defines a continuous function for every $f\in L^2(G)$.

Now fix $k\in C(G)$ satisfying

Define the right-convolution operator $T:L^2(G)\to L^2(G)$ by

Equivalently, $T$ is Hilbert–Schmidt with kernel $K(g,r)=k(r^{-1}g)$, and the symmetry assumption implies $K(g,r)=\overline{K(r,g)}$, so $T$ is self-adjoint and compact.

Lemma. Let $k$ and $T$ be as above. For each $\alpha\in\mathbb{R}\setminus\{0\}$, the eigenspace

$$ H_\alpha=\{f\in L^2(G): Tf=\alpha f\} $$

is contained in $E_{\mathrm{fin}}$.

Proof. Since $T$ is compact and self-adjoint, $H_\alpha$ is finite-dimensional. Moreover, $H_\alpha\subseteq C(G)$: if $Tf=\alpha f$ with $\alpha\neq 0$, then $f=\alpha^{-1}Tf$ and $Tf$ is continuous by the discussion above.

The space $H_\alpha$ is invariant under the left regular representation. Indeed, for $g\in G$,

so if $Tf=\alpha f$, then $T(\lambda(g)f)=\alpha\,\lambda(g)f$ and $\lambda(g)f\in H_\alpha$.

Let $\{f_1,\dots,f_r\}$ be an orthonormal basis of $H_\alpha$. Define continuous functions

Since $\lambda(g)f_i\in H_\alpha$, we can expand

Thus $g\mapsto (\theta_{ij}(g))_{i,j}$ is the matrix of the unitary operator $\lambda(g)|_{H_\alpha}$ in the basis $\{f_i\}$, so it defines a finite-dimensional unitary representation $\rho$ of $G$ on $\mathbb{C}^r$.

Finally, evaluating at the identity element $e\in G$ gives

so each $f_i$ is a linear combination of the coefficient functions $\theta_{ki}(g^{-1})$. Since $E_{\mathrm{fin}}$ is closed under inversion, we conclude $f_i\in E_{\mathrm{fin}}$. $\square$

Lemma. Let $k$ and $T$ be as above. Then for every $f\in L^2(G)$ we have

$$ Tf\in \overline{E_{\mathrm{fin}}}^{\|\cdot\|_2}. $$

In particular, $Tf$ can be approximated in $L^2$ by elements of $E_{\mathrm{fin}}$.

Proof. Let $\{ \phi_n \}$ be a complete orthonormal set of eigenvectors for the nonzero eigenspaces of $T$, with eigenvalues $\alpha_n\ne 0$:

Then by the spectral theorem for compact self-adjoint operators, any $f\in L^2(G)$ can be written as

with $\sum_n |c_n|^2<\infty$. Hence

Approximating this series by partial sums yields $L^2$-convergence, and each $\phi_n\in E_{\mathrm{fin}}$ by the previous lemma. Thus $Tf$ is in the $L^2$-closure of $E_{\mathrm{fin}}$. $\square$

Lemma (Smoothing upgrades to uniform approximation). Let $k\in C(G)$ satisfy $k(g)=\overline{k(g^{-1})}$ and let $T:L^2(G)\to L^2(G)$ be right-convolution by $k$:

$$ Tf=f*k. $$

Then for every $f\in L^2(G)$ we have

$$ Tf\in \overline{E_{\mathrm{fin}}}^{\|\cdot\|_\infty}\subseteq C(G). $$

Proof. Since $T$ is compact and self-adjoint, it has nonzero eigenvalues $\alpha$ with finite-dimensional eigenspaces

and $L^2(G)=\ker T \oplus \bigoplus_{\alpha\ne 0} H_\alpha$ orthogonally. For $\varepsilon>0$, define the finite-rank truncation by eigenspaces

where the sum ranges over nonzero eigenvalues $\alpha$ of $T$ and $P_\alpha$ is the orthogonal projection onto the eigenspace $H_\alpha=\{f: Tf=\alpha f\}$. Since $\alpha\to 0$, the sum is finite, so $T_\varepsilon$ has finite rank and $T_\varepsilon f\in E_{\mathrm{fin}}$.

Moreover, each $H_\alpha$ is $\lambda$-invariant, hence $P_\alpha$ (and therefore $T_\varepsilon$) commutes with $\lambda$. Since $T_\varepsilon$ has finite rank and maps into $C(G)$, it has a continuous kernel $K_\varepsilon(g,r)$, and the commutation relation implies

Taking $t=r^{-1}$ gives $K_\varepsilon(g,r)=K_\varepsilon(r^{-1}g,e)$. Defining

we obtain $K_\varepsilon(g,r)=k_\varepsilon(r^{-1}g)$, i.e.

Now Cauchy–Schwarz gives, for every $g\in G$,

so

Finally, for the right-convolution operator $S_u(f)=f*u$ on a compact group one has $\|S_u\|_{\mathrm{HS}}=\|u\|_2$ (compute from the kernel $u(r^{-1}g)$), so

By the spectral theorem for compact self-adjoint operators,

so $\|k-k_\varepsilon\|_2\to 0$ and therefore $T_\varepsilon f\to Tf$ uniformly, with $T_\varepsilon f\in E_{\mathrm{fin}}$. $\square$

2.8. Approximate identities and density

We now use the existence of an approximate identity in $C(G)$.

Proposition (Approximate identity). If $G$ is compact, there exists a net $\{k_U\}\subset C(G)$ indexed by neighborhoods $U$ of $e\in G$ such that:

1. $k_U\ge 0$, $\mathrm{supp}(k_U)\subseteq U$,
2. $\displaystyle \int_G k_U(g)\,dg = 1$,
3. $k_U(g)=k_U(g^{-1})$,
4. for every $f\in C(G)$, both $k_U*f\to f$ and $f*k_U\to f$ uniformly on $G$.

Proof. (Existence.) Fix a neighborhood $U$ of $e$. Choose a symmetric neighborhood $V$ of $e$ with $\overline V\subset U$ (possible in a topological group). By Urysohn’s lemma, there exists $\psi\in C(G)$ with $0\le \psi\le 1$, $\psi\equiv 1$ on $\overline V$, and $\mathrm{supp}(\psi)\subset U$. Then $h(g):=\psi(g)+\psi(g^{-1})$ is continuous, nonnegative, symmetric, supported in $U$, and $\int_G h>0$. Setting $k_U:=h/\int_G h$ gives (1)–(3).

(Approximation.) Fix $f\in C(G)$ and $\varepsilon>0$. By uniform continuity of $f$ (compactness of $G$), there exists a neighborhood $W$ of $e$ such that

If $U\subseteq W$, then for all $g\in G$,

Thus $k_U*f\to f$ uniformly. The proof for $f*k_U\to f$ is the same, using uniform continuity of right translations. $\square$

Now let $T_U$ be the convolution operator

Each $k_U$ satisfies the hypotheses of the Hilbert–Schmidt lemmas above, and $T_Uf\to f$ uniformly for every $f\in C(G)$.

By the previous lemma, $T_Uf\in \overline{E_{\mathrm{fin}}}^{\|\cdot\|_\infty}$ for every $f\in L^2(G)$, hence in particular for $f\in C(G)$. Since $T_Uf\to f$ uniformly on $G$, we conclude

This proves the claim, and therefore completes the proof of the Peter–Weyl theorem. $\blacksquare$

3. Examples

3.1. The circle group SO(2)

We now spell out the Peter–Weyl theorem concretely for $G=\mathrm{SO}(2)$, showing that it reduces to classical Fourier series on the circle.

Identify $\mathrm{SO}(2)$ and its Haar measure

Every element of $\mathrm{SO}(2)$ is a rotation

Matrix multiplication corresponds to adding angles:

Hence $\mathrm{SO}(2)\cong \mathbb{T}\cong \mathbb{R}/2\pi\mathbb{Z}$ (a compact abelian group).

The normalized Haar measure is

so for $f\in L^1(\mathrm{SO}(2))$,

Irreducible unitary representations are characters

Since $G=\mathrm{SO}(2)$ is compact abelian, every irreducible unitary representation is $1$-dimensional (a character). Concretely, they are indexed by $n\in\mathbb{Z}$:

Each $\pi_n$ is unitary since $|e^{in\theta}|=1$, and irreducibility is automatic in dimension $1$. Thus

Matrix coefficients and the Peter–Weyl space $E_{\mathrm{fin}}$

For a representation $\pi$, a matrix coefficient has the form $g\mapsto \langle \pi(g)v,w\rangle$.

Here $\pi_n$ is $1$-dimensional, so its coefficient functions are exactly the characters themselves:

Therefore the Peter–Weyl subspace generated by finite-dimensional irreps is the space of trigonometric polynomials:

The left regular representation decomposes into Fourier modes

Identifying $\mathrm{SO}(2)\cong [0,2\pi)$ via $R_\varphi$, the left regular representation acts by translation:

For the Fourier modes $e_n(\varphi):=e^{in\varphi}$,

Thus each $\mathbb{C}e^{in\varphi}$ is $\lambda$-invariant and carries the character $\pi_{-n}$. Since $\{e^{in\varphi}\}_{n\in\mathbb{Z}}$ is an orthonormal basis of $L^2([0,2\pi),\frac{d\varphi}{2\pi})$, we get

(Here the last display just reindexes $n\mapsto -n$.)

Orthogonality relations

With the normalized Haar measure, the characters are orthonormal:

This is Schur orthogonality in the abelian case.

Separation of points and density in $C(\mathrm{SO}(2))$

If $R_\theta\neq R_0$, then $\theta\not\equiv 0\pmod{2\pi}$ and

so $\widehat G$ separates points (Peter–Weyl item (3)).

Moreover, Peter–Weyl item (4) says that the span of matrix coefficients is dense in $C(G)$ in the sup norm. Here this becomes:

i.e. trigonometric polynomials are uniformly dense in $C(\mathbb{T})$ (e.g. via Fejér kernels / Cesàro means of Fourier series).

Fourier transform and Plancherel (Parseval)

For $f\in L^1(\mathrm{SO}(2))$, the Peter–Weyl Fourier transform at $\pi_n$ is scalar-valued:

Writing $g=R_\theta$ gives $g^{-1}=R_{-\theta}$ and $\pi_n(g^{-1})=e^{-in\theta}$, hence

which is the usual Fourier coefficient $\widehat f(n)$.

Since $d_{\pi_n}=1$, Plancherel becomes the classical Parseval identity:

3.2. The rotation group SO(3)

We now spell out the Peter–Weyl theorem concretely for $G=\mathrm{SO}(3)$, where the Fourier basis is given by Wigner $D$-matrix coefficients.

Identify $\mathrm{SO}(3)$ and its Haar measure

Recall

a compact (non-abelian) Lie group.

Using Euler angles, every $g\in \mathrm{SO}(3)$ can be written (non-uniquely on a null set) as

With Haar measure normalized by $\mu(\mathrm{SO}(3))=1$, one has

so for $f\in L^1(\mathrm{SO}(3))$,

Irreducible unitary representations

The irreducible unitary representations of $\mathrm{SO}(3)$ are indexed by $\ell\in\mathbb{Z}_{\ge 0}$. Denote a choice of representative by

Equivalently, $\pi_\ell$ may be realized as the natural action on spherical harmonics of degree $\ell$. Thus

Matrix coefficients and the Peter–Weyl space $E_{\mathrm{fin}}$

Fix an orthonormal basis $\{e_m^\ell\}_{m=-\ell}^{\ell}$ of $\mathcal{H}_\ell$. The matrix coefficients of $\pi_\ell$ are

the (unitary) Wigner $D$-matrix elements. Therefore

The left regular representation decomposes into $D$-matrix blocks

For each $\ell$, the span of $\{D^\ell_{mn}\}_{m,n=-\ell}^\ell$ is a $\lambda$-invariant subspace of $L^2(\mathrm{SO}(3))$ isomorphic to $\mathcal{H}_\ell\otimes \mathcal{H}_\ell^*$. In particular, each $\pi_\ell$ occurs in the left regular representation with multiplicity $d_\ell$:

Orthogonality relations

Schur orthogonality specializes to

Equivalently, $\{\sqrt{2\ell+1}\,D^\ell_{mn}\}$ is an orthonormal basis of $L^2(\mathrm{SO}(3))$.

Separation of points and density in $C(\mathrm{SO}(3))$

The standard representation $\pi_1(g)=g$ on $\mathbb{R}^3$ (and hence on $\mathbb{C}^3$ by complexification) is the $\ell=1$ irreducible representation. Its matrix coefficients are the coordinate functions $g\mapsto g_{ij}$, which clearly separate points: if $g\neq h$ then $g_{ij}\neq h_{ij}$ for some $i,j$. Moreover,

Fourier transform and Plancherel (Parseval)

For $f\in L^1(\mathrm{SO}(3))$, the Peter–Weyl Fourier transform at $\pi_\ell$ is matrix-valued:

In the basis above,

Plancherel becomes

4. Group Convolutional Neural Networks

We are interested in studying learnable functions that satisfy certain symmetries. In particular, we want to study functions that are equivariant with respect to the action of a compact group $G$.

Definition (Equivariant function). Let $G$ be a compact group acting on functions $f\in L^2(G)$ by left translation:

$$(\lambda(g)f)(h) = f(g^{-1}h), \quad g,h \in G.$$

A linear operator $F$ is $G$-equivariant if

$$ F(\lambda(g) f) = \lambda(g) (F f) \qquad \forall g \in G, f \in L^2(G). $$

Definition (Group convolution). Define the (right) convolution with a kernel $L$ by

$$ (Ff)(h) = (f \ast L)(h) = \int_G f(hg^{-1}) L(g) \, d\mu(g). $$

Equivariant operators are exactly right-convolutions with suitable kernels.

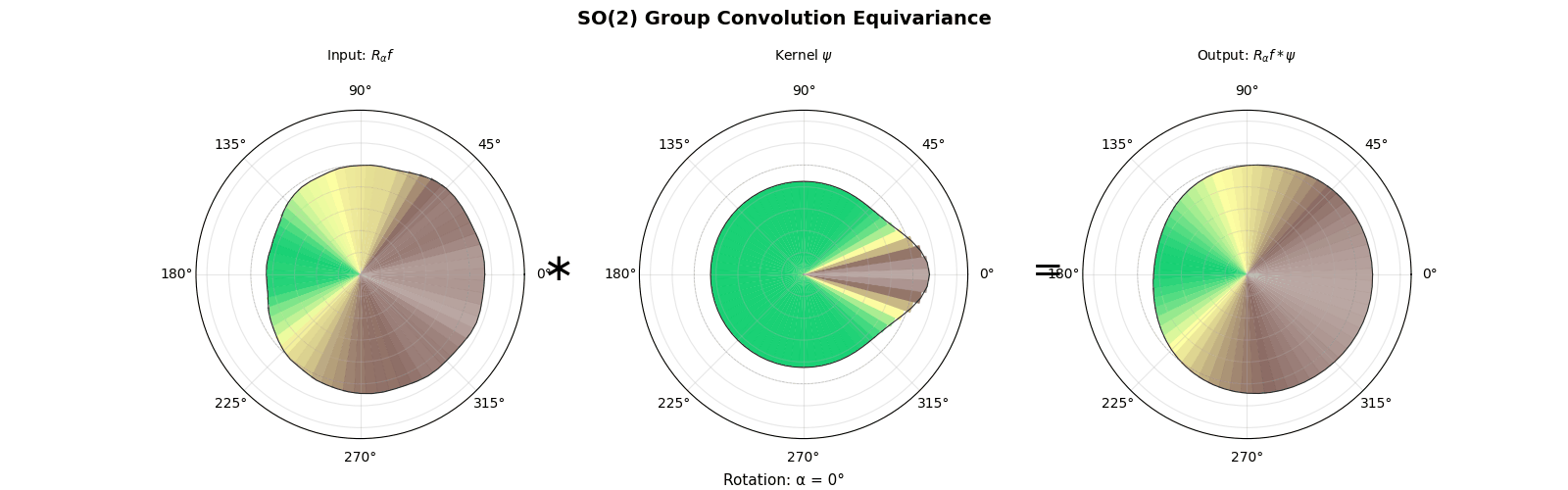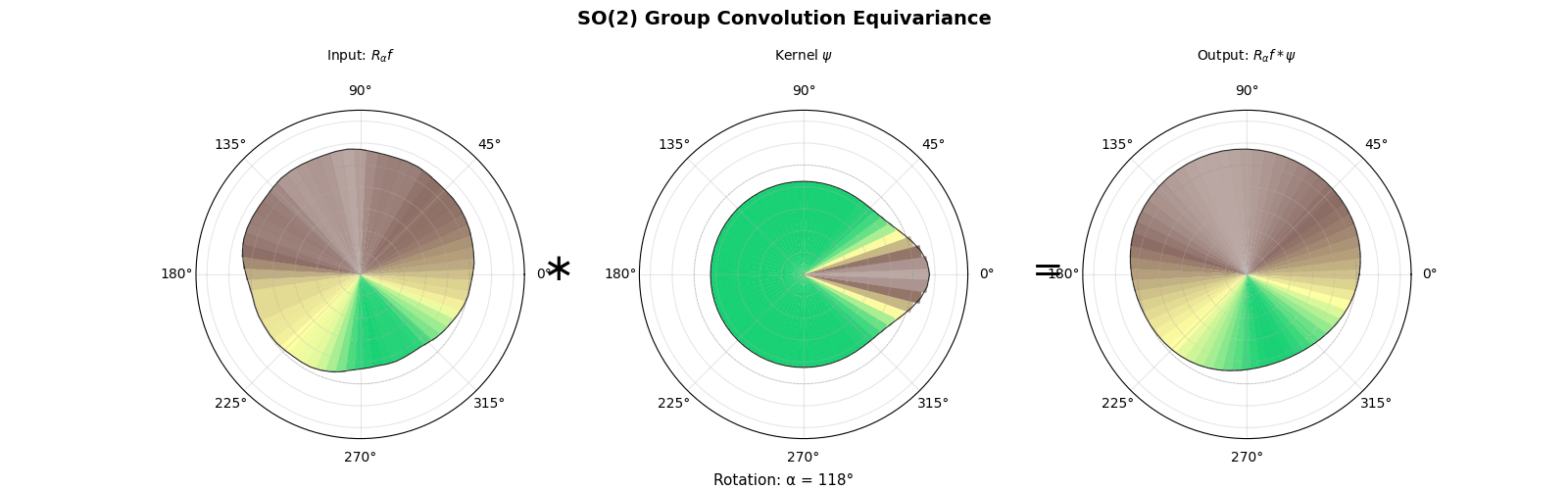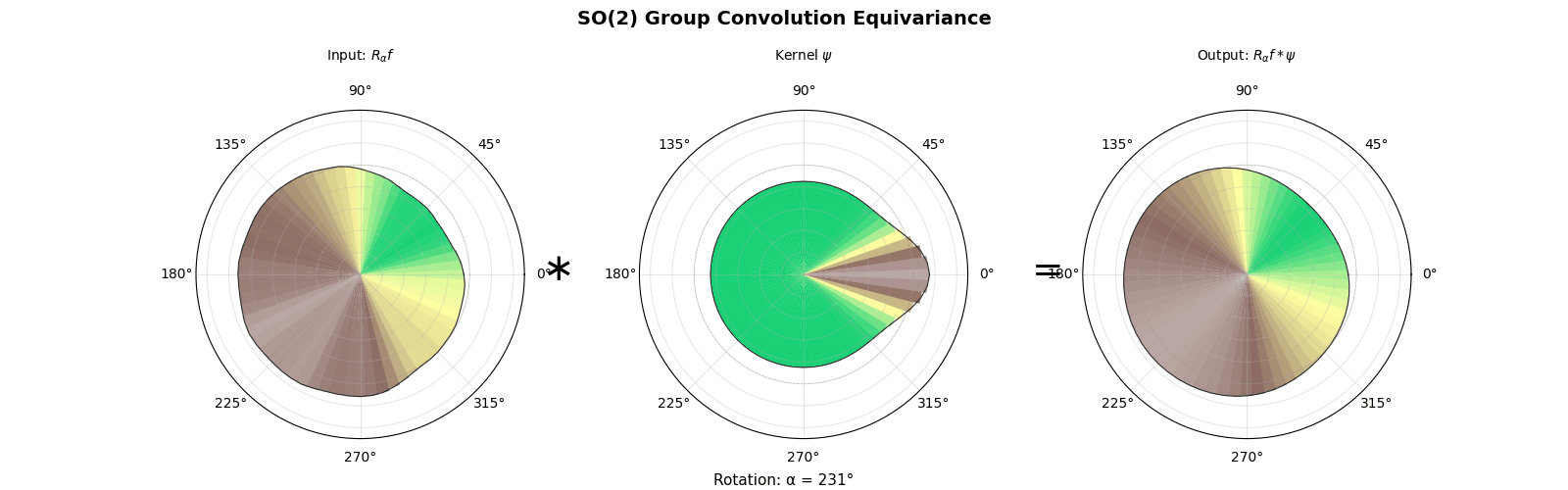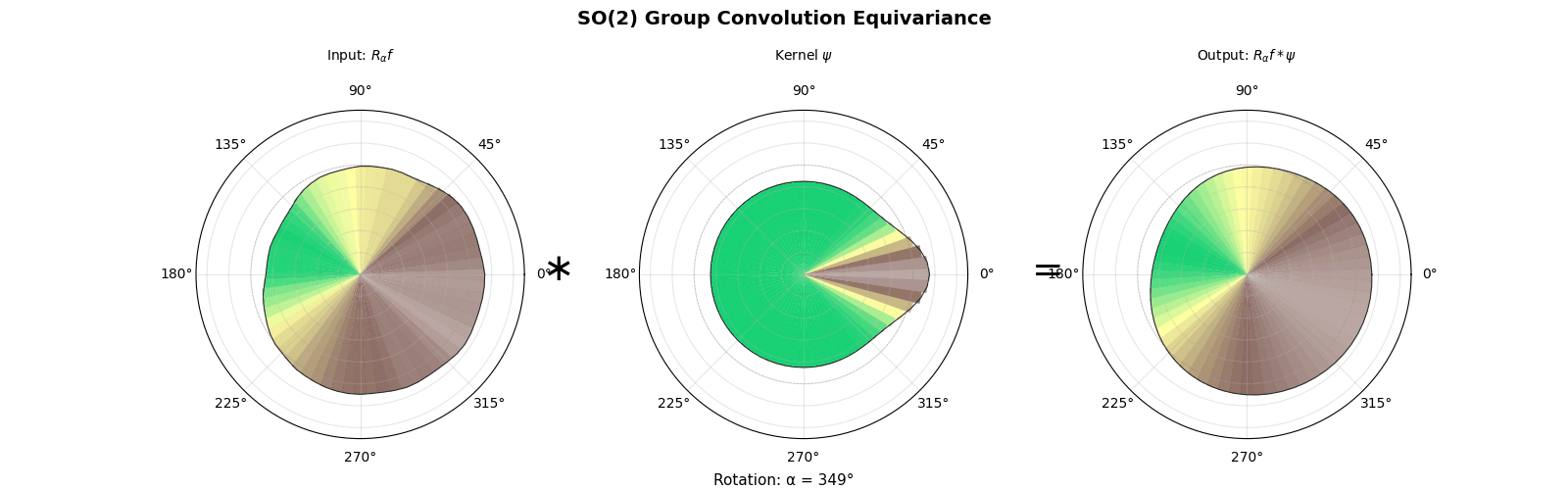
4.1 Example SO(2)

In the example $G = \mathrm{SO}(2)$, using a change of variables $d\mu = \frac{d\theta}{2\pi}$. The formula becomes

which is the classical convolution on the circle.

Fourier transform of group convolutions

However, the Peter-Weyl theorem allows us to change the viewpoint and improve the efficiency of computations. Indeed,

where $\widehat{L}(\pi)$ is a $d_\pi \times d_\pi$ matrix. In the abelian case $d_\pi=1$ so this is scalar multiplication, but for non-abelian groups the matrix product order matters.

Example using $G = \mathrm{SO}(2)$, we have $d_{\pi_n} = 1$ for all $n \in \mathbb{Z}$:

import numpy as np

N = 64
theta = np.linspace(0, 2*np.pi, N, endpoint=False)  # Discretize SO(2) ~ [0, 2π)
dtheta = 2 * np.pi / N

f = np.sin(3*theta) + 0.5*np.cos(5*theta) # Example signal f(θ) on the circle
L = np.exp(-0.5 * (((theta + np.pi) % (2*np.pi) - np.pi) / 0.5)**2)

# Method A: Direct discretized integral (O(N^2))
# (Ff)(θ_k) ≈ (1/(2π)) Σ_{j=0}^{N-1} f(θ_k - θ_j) L(θ_j) dθ
conv_direct = np.empty(N)
j = np.arange(N)

for k in range(N):
    idx = (k - j) % N # f(θ_k - θ_j) corresponds to f[(k-j) mod N] on the grid
    conv_direct[k] = (1/(2*np.pi)) * np.sum(f[idx] * L) * dtheta

# Method B: Fourier / Peter–Weyl (FFT) (O(N log N))
# ifft(fft(f) * fft(L))[k] = Σ f[k-j] L[j]
# We still multiply by 1/(2π) to match the integral's factor.
f_hat = np.fft.fft(f)
L_hat = np.fft.fft(L)

conv_fft = np.fft.ifft(f_hat * L_hat).real * dtheta / (2*np.pi)

# Check agreement
max_err = np.max(np.abs(conv_direct - conv_fft))
print("Max |direct - fft| =", max_err)

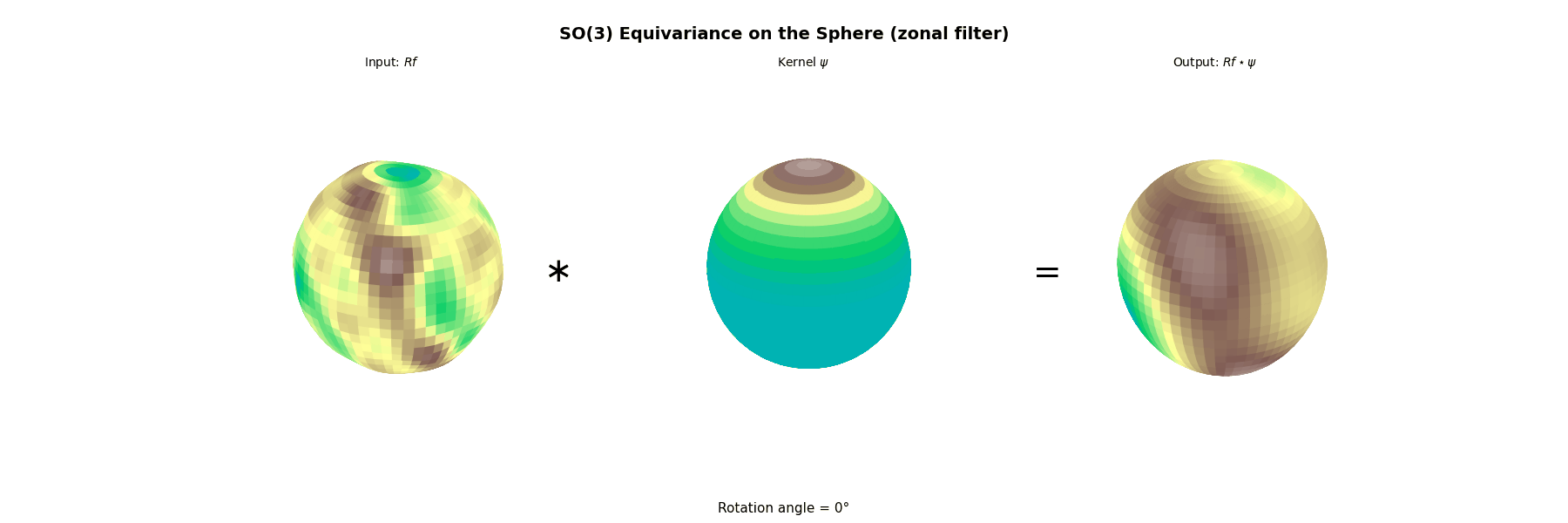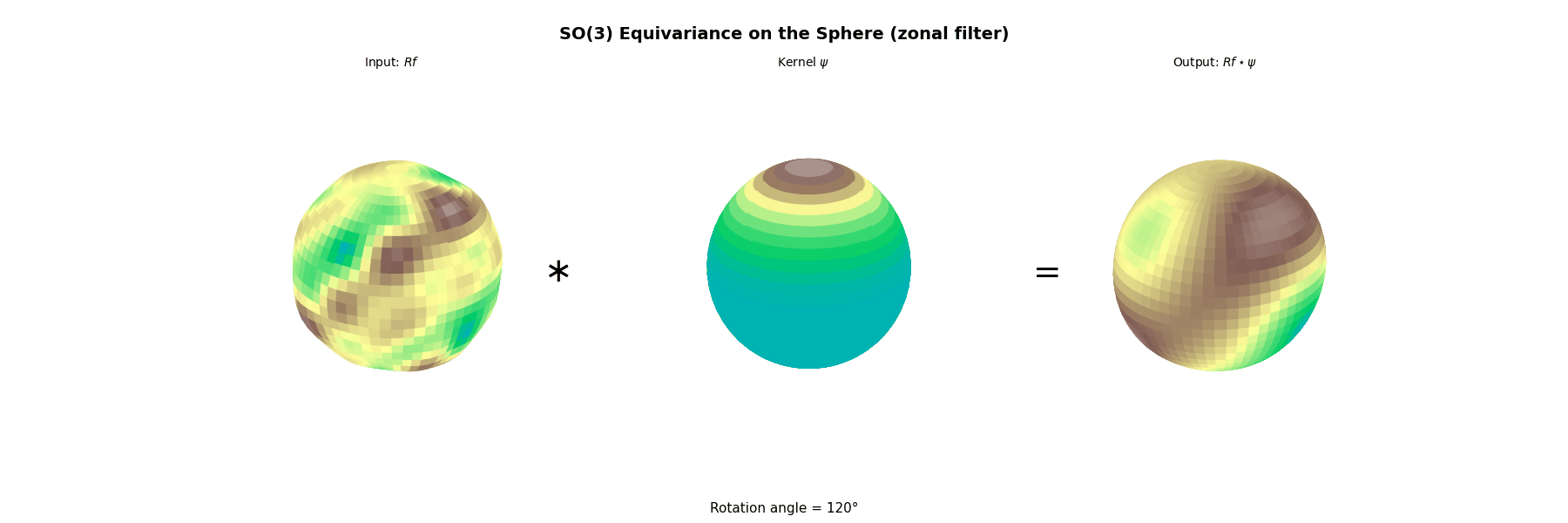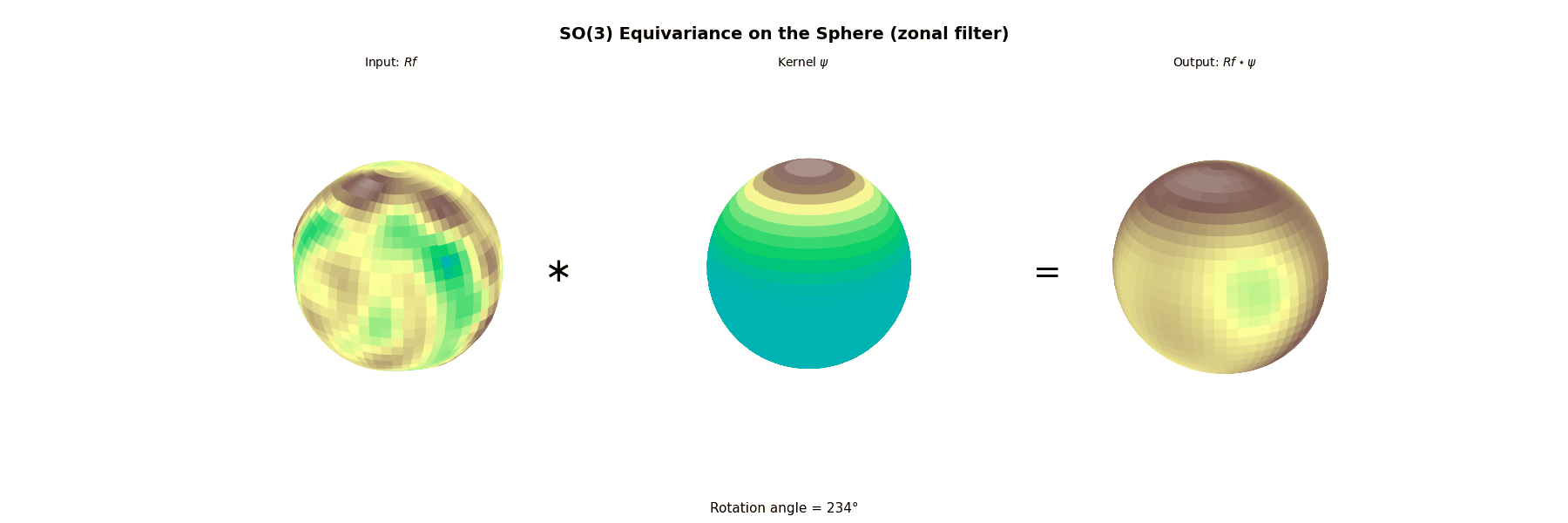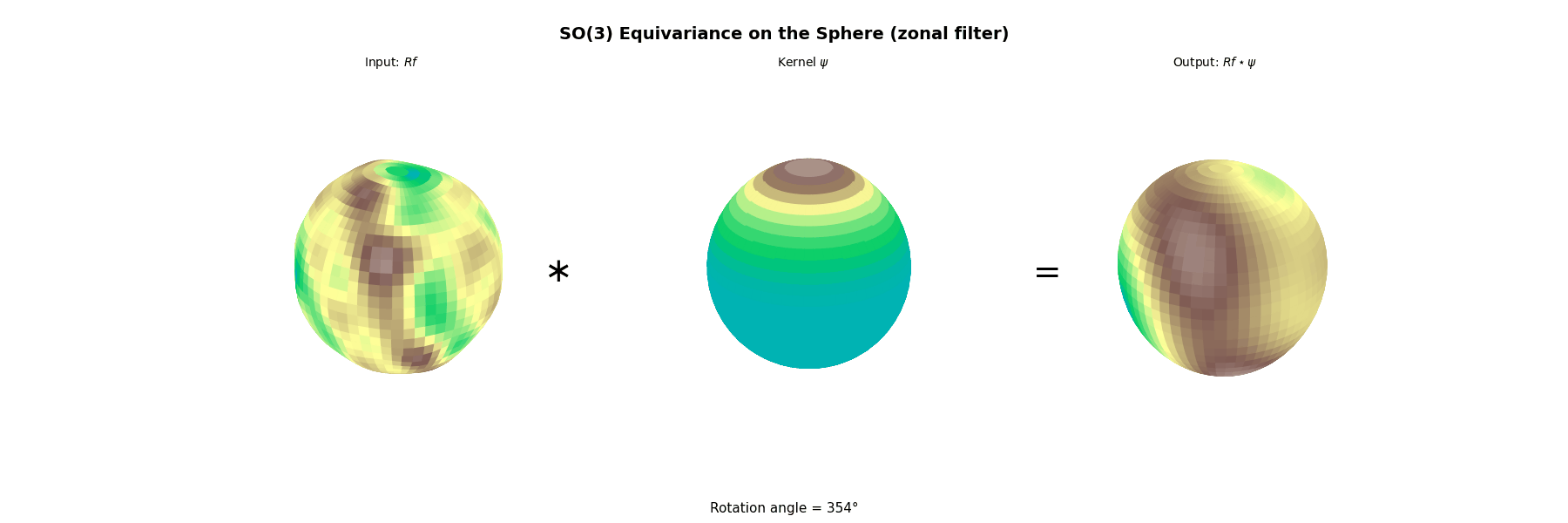
4.2. Example SO(3)

Let $G=\mathrm{SO}(3)$ with normalized Haar measure

in $ZYZ$ Euler angles $g=R_z(\alpha)R_y(\beta)R_z(\gamma)$.

For $\ell\in\mathbb{Z}_{\ge 0}$ let $D^\ell(g)\in\mathbb{C}^{(2\ell+1)\times(2\ell+1)}$ denote the Wigner $D$-matrix of the irreducible representation $\pi_\ell$, with entries

where $d^\ell(\beta)$ is the (real) small Wigner $d$-matrix.

With the Peter–Weyl Fourier transform convention

the (right) group convolution

satisfies the convolution theorem

which is a matrix product (and is not commutative in general).

Numerically, one can discretize $(\alpha,\beta,\gamma)$ on a tensor grid, approximate integrals using quadrature weights proportional to $\sin\beta$, and truncate the inverse transform to $\ell\le L_{\max}$:

In code, the spectral convolution step is literally matrix multiplication at each frequency $\ell$:

alpha, beta, gamma, weights, rotations = make_euler_zyz_grid(N_ALPHA, N_BETA, N_GAMMA) # Helper functions.

f = create_signal(rotations)
L = normalize_kernel(create_kernel(rotations), weights)

D_grid = precompute_wigner_D_grid(alpha, beta, gamma, L_MAX)

f_hat = fourier_coefficients_from_samples(f, D_grid, weights)
L_hat = fourier_coefficients_from_samples(L, D_grid, weights)

conv_hat = {ell: L_hat[ell] @ f_hat[ell] for ell in f_hat}
conv = inverse_fourier_on_grid(conv_hat, D_grid, L_MAX)

References

[-1] The code is available at: https://github.com/dani2442/dani2442_code/tree/main/group-cnn

[0] Dana P. Williams, The Peter–Weyl Theorem for Compact Groups, notes. https://math.dartmouth.edu/~dana/bookspapers/pw.pdf

[1] Elias M. Stein, Topics in Harmonic Analysis Related to the Littlewood–Paley Theory, Annals of Mathematics Studies, Princeton University Press.

[2] Walter Rudin, Fourier Analysis on Groups, Wiley Classics Library, John Wiley & Sons.

[3] Gerald B. Folland, A Course in Abstract Harmonic Analysis, Studies in Advanced Mathematics, CRC Press.